SolidWorks: 4 usos en la ingeniería

SolidWorks es un software CAD, esto quiere decir que es un software de diseño asistido por computadora. En otras palabras, Solidworks es un software que nos permite realizar diferentes tipos de diseños de manera intuitiva y eficiente.

En la actualidad existen muchos programas CAD, sin embargo SolidWorks es uno de los más usado debido a la gran cantidad de herramientas y paquetes que posee. Este software es uno de los más importantes en el mundo de la ingeniería y el diseño junto a AutoCAD.

Aunque SolidWorks es usado principalmente en el mundo de la ingeniería, vale mencionar, que también es usado en otros ámbitos como en la moda, el deporte, creación de accesorios y diferentes tipos de proyectos a grande o pequeña escala. 

Es importante aclarar que SolidWorks tiene muchos usos, todo depende de las necesidades. Los usos que aquí nombramos son los más básicos y los más aplicados, sin embargo el mundo de SolidWoks es muy amplio.

Proceso de diseño en SolidWorks. Fuente: adrformacion SolidWorks

Usos de SolidWorks

Realizar croquis 2D (bidimensional) o planos

Una de las principales ventajas que tiene SolidWorks es la facilidad de transformar diseños de 2D (bidimensionales) a 3D (tridimensionales) y viceversa, algo que en AutoCAD, por ejemplo, no es tan fácil. 

Gracias a los procesos y las herramientas intuitivas que tiene SolidWorks es posible plasmar y obtener planos mediante diseños tridimensionales o, de manera inversa, lograr realizar diseños tridimensionales mediante planos o croquis.

El fuerte de SolidWorks son sus herramientas para realizar modelos y estudios tridimensionales pero esto no quita la gran utilidad que tiene en la generación de croquis y planos. SolidWorks es un excelente aliado al momento de obtener diferentes planos con sus normas, leyendas y características especificas.

Croquis realizado en SolidWorks. Fuente: UDDIMSI - SolidWorks, canal de YouTube.

Realizar modelos 3D (tridimensional)

El fuerte de SolidWorks, como herramienta CAD, es el permitirnos realizar modelos tridimensionales de forma rápida, intuitiva y eficiente.

El software nos permite realizar piezas tridimensionales pero además de esto nos permite ensamblar diferentes piezas para obtener una máquina compuesta. Es decir, con esta herramienta podemos realizar piezas simples y piezas compuestas. Las herramientas para el ensamblaje que tiene el software permite que este proceso sea bastante fácil e intuitivo de realizar.

En la ingeniería, el poder realizar diseños y modelos tridimensionales, y además poder incluir la posibilidad del ensamblaje, es de mucha utilidad porque permite observar, mejorar y optimizar un producto sin la necesidad de tener que construirlo en físico o sin tener que gastar cierta cantidad de recursos.

Diseño 3D en SolidWorks. Fuente: Studioseed - Diseño en SolidWorks

Estudio de cargas

Esta aplicación se aplica mucho en el ámbito ingenieril. El estudio de cargas nos permite observar el comportamiento de nuestro diseño mecánico bajo el efecto de diferentes cargas (fuerzas y esfuerzos). Esto es fundamental para saber si nuestro diseño mecánico en realidad va a lograr cumplir el objetivo para el cual fue diseñado.

En el estudio de cargas, tenemos que SolidWorks nos permite observar los puntos donde el esfuerzo es mayor o donde el esfuerzo es menor. Gracias a esto podemos rediseñar y optimizar el producto que estamos modelando. Al realizar este estudio tenemos que SolidWorks de manera directa nos proporciona una escala de colores en donde nos muestra los puntos críticos del diseño al recibir una carga.

En la ingeniería la eficiencia es fundamental, es por ello que el análisis de cargas nos permite observar una variable de gran importancia: el sobrediseño. El sobrediseño ocurre cuando el diseño que estamos realizando esta muy por encima de las especificaciones que deseamos, en el estudio de cargas podemos observar estos problemas y eliminarlos.

Análisis de carga. Fuente: SolidWorks blog.

Realizar animaciones/simulaciones

SolidWorks tiene una aplicación conocida como ''SolidWorks Motion''. Esta herramienta es de gran utilidad para observar el comportamiento de un diseño en movimiento, es decir, nos permite hacer una simulación.

Con esta simulación podemos estudiar diferentes variables, como ejemplo: que no haya interferencia entre las diferentes piezas/partes, la potencia de los motores, el comportamiento del diseño frente a cargas dinámicas (debido al movimiento) y otras similares.

La simulación, en la ingeniería, es de suma importancia ya que nos permite observar el comportamiento de nuestro diseño en movimiento y en acción. Además, el software nos permite generar diferentes vídeos que son de gran utilidad en las presentación y estudio de nuestro diseño ingenieril. 

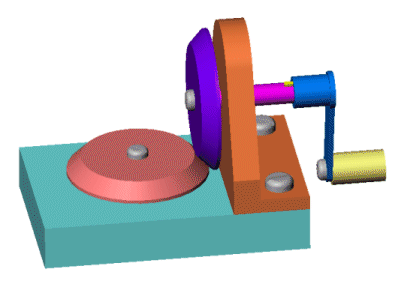
Animación en SolidWorks. Fuente: SolidWorks Help.

Referencias

1.  Web Oficial de Solidworks (en inglés)
2.  Web Oficial de Solidworks (en castellano)

Read More

Problema de crédito e intereses.

Problema: Pamela quiere obtener un préstamo de S/10000 para modelar su casa. Se le ofrecen tres crediticias que son:

1. Presto fácil, un interés del 12% semestral y un tiempo de 6 años.
2. Pago al toque, un interés del 5.5% trimestral y un tiempo de 7 años.
3. Deuda cero, un interés del 1.85% mensual y un tiempo de 78 meses.

Para resolver este problema buscaremos el interés compuesto que se debe pagar a cada institución. Usaremos la siguiente formula: 

i = C·[(1 + i)^(n) - 1] 

Donde:

• i = interés
• C = capital pedido
• n = periodo de tiempo basado en el tipo de interés  

Procedemos a calcular el interés para cada empresa: 

1) Presto fácil: el interés es 12% semestral por ende debemos colocar el periodo de tiempo en semestre.

i = (10000)·[(1 + 0.12)^(12) - 1] 

i = (10000)·(2.89)

i = S/28959.75

2) Pago al toque: el interés es del 5.5% trimestral por ende debemos colocar el periodo de tiempo en trimestre.

i = (10000)·[(1 + 0.0055)^(28) - 1] 

i = (10000)·(3.47)

i = S/34778.43

3)Deuda cero: en interés es del 1.85% mensual por ende debemos colocar el periodo de tiempo en meses.

i = (10000)·[(1 + 0.018)^(78) - 1] 

i = (10000)·(3.02)

i = S/30209.31

Finalmente, la mejor opción es elegir las condiciones de préstamo de Presto fácil, esto es debido a que con esta institución pagaremos menos interés.

Créditos:

• Este problema fue sacado de la página de Facebook: Brainlat.

En caso de usar esta resolución para otras páginas es fundamental indicar el enlace de este blog.

Read More

Variables directamente proporcionales e inversamente propoporcionales.

Problema: Analiza los datos presentados en la tabla, calcula el cociente constante y el producto constante y determine si son cantidades inversamente proporcionales o directamente proporcionales. 

Para resolver este problema debemos seguir los siguientes pasos:

1. Identificar si los datos son inversa o directamente proporcionales.
2. Si los datos son directamente proporcionales entonces se calcula el cociente constante.
3. Si los datos son inversamente proporcionales entonces se calcula el producto constante.

Seguimos el procedimiento descrito: 

1) Observando los datos podemos observar que son inversamente proporcionales. Esto se sabe porque mientras los valores -x- aumentan los valores de -y- disminuyen, es decir, el comportamiento es inverso.

2) Como los datos son inversamente proporcionales debemos calcular el producto constante, se usa la siguiente ecuación: 

y = k/x ; Ecuación para variables inversamente proporcionales 

Procedemos a calcular la constante, elegimos cualquier par ordenado:

k = y·x 

k = (24)·(1) 

k = 24 

Por tanto, el producto constante viene siendo 24. 

Si quieres aprender más sobre la relación entre magnitudes te dejo este enlace: 

• https://300mots.blogspot.com/2019/08/magnitudes-correlacionadas.html

Créditos:

• Este problema fue sacado de la página de Facebook: Brainlat.

En caso de usar esta resolución para otras páginas es fundamental indicar el enlace de este blog.

Read More

Problema: recta tangente y elipse.

Determine el valor de -p- de modo que la recta y = x +p  sea tangente a la elipse x²+2y² = 6.

Inicialmente tenemos dos funciones:

• y = x + p ; ecuación de la recta
• x²+2y² = 6 ; ecuación de la elipse

Para resolver este problema vamos aplicar dos condiciones: 

1. Igualar la derivada de cada función, ya que la derivada representa la tangencia.
2. Igualar las funciones, esto porque ambas tienen un punto en común.

Procedemos a calcular las derivadas:

y = x + p;
y' = 1

Para el elipse, por comodidad, despejamos la variable -y- y luego derivamos:

x²+2y² = 6
x²+2y² = 6
2y² = 6 -x²
y² = 3 - x²/2
y = √(3 - x²/2)

Derivamos:

y = (3-x²/2)¹/²
y' = (1/2)·(3-x²/2)⁻¹/²·(-x)
y' = (-x/2)/√(3 - x²/2)


Procedemos a igualar las pendientes:

• (-x/2)/√(3 - x²/2) = 1  .......... ecuación 1

Como las funciones son tangentes aplicamos la segunda condición:

• √(3 - x²/2) = x + p ............. ecuación 2

Lo que haremos será resolver este sistema, para ello despejaremos a -x- de la ecuación 1:


(-x/2)/√(3 - x²/2) = 1
-x/2 = √(3 - x²/2)
x²/4 = 3 - x²/2
x²/2 + x²/4 = 3
3x²/4 = 3
x = √4
x = ±2 , tenemos dos soluciones


Veamos que tenemos dos soluciones, para saber cuál condición en verdad nos da la recta tangente debemos sustituir las soluciones en la derivada de la elipse y ver si cumplen la igualdad:


(-x/2)/√(3 - x²/2) = 1
(-2/2)/√(3 - (2)²/2) = 1
-1/1 = 1
-1 ≠ 1 ; por tanto x = +2 no cumple la igualdad

(-(-2)/2)/√(3 - x²/2) = 1
(2/2)/√(3 - (-2)²/2) = 1
1/1 = 1
1 ≠ 1 ; por tanto x = -2 si cumple la igualdad

Finalmente, procedemos a buscar el valor de -p- con el valor que cumple la igualdad:

p = √(3 - x²/2) - x
p = √(3 - (-2)²/2) - (-2)
p = 3 ; siendo este el valor necesario para que exista tangencia


Se debe cumplir que p = ±3 para que y = x + p sea tangente a la elipse x²+2y² = 6. 

Las rectas tangentes serían:

• y = x + 3 
• y = x - 3

Créditos:

• Este problema fue sacado de la página de Facebook: Brainlat.

En caso de usar esta resolución para otras páginas es fundamental indicar el enlace de este blog.

Read More

Problema: ángulos internos y externos de una circunferencia.

Del gráfico, calcula -x- si A, B, C y D son puntos de tangencia.

Para resolver el problema a continuación debemos plantear formulas asociadas al ángulo interno y ángulo externo de una circunferencia.


Si tenemos lo siguiente (ángulo externo):

Entonces podemos afirmar que:

∝ + AB = 180º 


Si tenemos lo siguiente (ángulo interno):

Entonces podemos afirmar que:

∝ = (AC + ED)/2


Para resolver nuestro problema usaremos estas definiciones.

1) Aplicamos definición de ángulo externo:

60º + CD = 180º ; CD = 120º 
70º + BA = 180º; BA = 110º 

2) Aplicamos definición de ángulo interno:

x = (CD + BA)/2
x = (120º + 110º) /2
x = 230º/2
x = 115º 

Por tanto, podemos afirmar que el ángulo -x- tiene un valor de 115º. Opción E.


Créditos:

• Este problema fue sacado de la página de Facebook: Brainlat.

En caso de usar esta resolución para otras páginas es fundamental indicar el enlace de este blog. 

Read More

Problema: Un conductor tiene una resistencia de 80 ohms ¿Cuál es la corriente si el conductor se conecta a una batería de 20 voltios?

La corriente que circular por el conductor es de 0.25 amperes. Sabiendo que tiene una resistencia de 80 ohms y se conecta a una batería de 20 voltios.


Respuesta:

Para resolver este problema debemos aplicar la ley de Ohm, esta nos dice que:

V = I·R

Donde:

• V = voltaje
• I = intensidad de corriente
• R = resistencia

Usaremos esta ecuación y obtendremos la intensidad de corriente:

(20 V) = I·(80 Ω)
I = 20 V / 80 Ω
I = 0.25 A 

Por tanto, podemos afirmar que la corriente que circular por el conductor viene siendo de 0.25 amperes.

Read More

Problema: Un buzo desea sumergirse a 30 m de profundidad, pero necesita saber la presión hidrostática a dicha profundidad, pues bien sabe que solo puede soportar 250,000 Pa. ¿Podrá sumergirse?

No, el buzo no podrá sumergirse hasta los 30 metros de profundidad. En esta profundidad tenemos que la presión hidrostática sobrepasa a la presión que se puede soportar.


Resolución:

Para resolver este problema debemos aplicar teoría de presión hidrostática. La misma se define como:

P = d·g·h

Donde:

• P = presión
• d = densidad
• g = gravedad
• h = profundidad

Entonces, aplicando esta ecuación, sabiendo que el fluido es agua, calculamos la presión a los 30 m:

P = (1000 kg/m³)·(9.8 m/s²)·(30)
P = 294,000 Pa

Como 294,000 Pa > 250,000 Pa podemos concluir que el buzo NO puede sumergirse hasta los 30 metros puesto que no soportaría la presión a esa profundidad.

Read More

¿Por qué no hay mujeres representadas en la pintura del Cabildo abierto del 22 de mayo?

En la pintura Cabildo abierto no hay mujeres porque para esa época (1810) las mujeres no podían entrar en los cabildos ni participar en ellos, es decir, las mujeres no tenían un representante en el cabildo.

La obra Cabildo abierto fue realizada por el artista chileno Pedro Subercaseaux. En esta obra se desea mostrar el cómo eran las situaciones o los debates en un cabildo abierto, sobre todo el cómo era la atmósfera. Este se inspiro en un cabildo abierto realizado en Buenos Aires el 22 de mayo de 1810. El cabildo abierto que se realizo en este fecha fue fundamental para la Revolución de Mayo.

Read More

¿Cuál es el significado de hiperpoderoso?

El significado de hiperpoderoso viene siendo: alguien o algo muy poderoso, es decir, con exceso de poder.

Persona hiperpoderosa. Fuente: freepik

Estudio de la palabra hiperpoderoso

Tengamos en cuenta que la palabra hiperpoderoso es compuesta, para lograr entender a la misma es fundamental el reconocer y entender cada parte:

1. Hiper-: este es un prefijo pues se encuentra antes de la palabra base, su utilidad es denotar superioridad o exceso.
2. -poderoso: viene siendo la palabra base, en este caso poderoso hace referencia a alguien o algo que tiene poder. 

Ejemplos de usos de la palabra hiperpoderoso

Conociendo cada parte de la palabra podemos afirmar que el significado de hiperpoderoso hace referencia a alguien o un objeto que tiene mucho poder. Veamos algunos ejemplos: 

1. Superman es hiperpoderoso.
2. Ese material puede generar una energía hiperpoderosa.
3. El universo tiene una esencia hiperpoderosa.

Vale decir que hiperpoderoso puede ser un sinónimo para superpoderoso.

Dato importante 

El prefijo hiper (sin tilde) tiene una función distinta al acortamiento híper (con tilde), el primero es un prefijo y el segundo es un acortamiento para la palabra hipermercado.

Uso de hiper- e híper. Fuente: Apuntes ortográficos.

Read More

Cuerpo rígido.

Cuerpo rígido: un cuerpo rígido es aquel que a pesar de recibir fuerzas externas no se deforma. Sin embargo, esto se cumple en condiciones reales, los cuerpos rígidos, en algún punto, se llegan a deformar.

Algunos ejemplos de cuerpos rígidos son:

• Una esfera de plomo.
• La estructura de un automóvil.
• Un cubo de concreto.
• La estructura de una construcción.

Es importante considerar que un cuerpo rígido no es mas que un modelo ideal, ya que en la realidad la rigidez es relativa y no absoluta. El modelo asociado a un cuerpo rígido es fundamental en la cinemática y mecánica.

Los cuerpos rígidos pueden tener dos modos de movimientos que son: 

• Traslación: ocurre cuando todos los puntos del cuerpo tienen la misma velocidad y aceleración.
• Rotación: ocurre cuando todos los puntos del eje se mueven respecto a un eje especifico, en este caso se mantiene la velocidad y aceleración angular.

Read More

Prefijos y sufijos.

Tanto los prefijos como los sufijos son modificadores gramaticales de una palabra conocida como raíz o primitiva. Los prefijos van antes de la raíz y los sufijos después de la raíz.

Veamos un ejemplo:  ¿La palabra paraguas lleva prefijo o sufijo?

En este caso la palabra paraguas tiene un prefijo. La palabra se puede desglosar como:

• Prefijo: para-
• Raíz: agua.

El paraguas es un instrumento o herramienta que sirve para protegerse del agua, este instrumento para (detiene) el agua, de ahí su nombre.

Entonces, podemos afirmar que la palabra paraguas lleva prefijo, siendo agua la palabra raíz. 

La familia léxica de una palabra se caracteriza, principalmente, por tener el mismo lexema, sin embargo, con la introducción de prefijos y sufijos es posible obtener una serie de palabras derivadas, estas palabras derivadas son la familia léxica de la palabra base.

Read More

Factores que influyen en el clima de Ecuador.

Los principales factores que definen el clima que tenemos en el Ecuador son:

1. Las formas de relieve.
2. La ubicación entre los trópicos.
3. Las altitudes.
4. Las corrientes de viento.
5. La distribución de la tierra y el agua.

Se puede afirmar que el clima es un sistema dinámico, esto porque se encuentra en constante cambio y adaptación; hay climas fríos, climas de estaciones secas, climas de humedad y calor. El clima, como concepto general, desde hace muchos años sigue siendo dinámico y cambiante.

Un sistema dinámico es el que evoluciona o cambia con el tiempo (periodos). El clima tiene que ver con la humedad, la temperatura, los vientos y otras variables, y esto determina el estado de la atmósfera en un punto determinado de la tierra.

Por otra parte, Ecuador es un país del Sur de América, el mismo cuenta con 24 provincias bien definidas.

Este país posee una gran riqueza natural, sobre todo por la diversidad de relieve y clima que posee. La cordillera de los Andes pasa por el medio del país, esta genera gran cantidad de recursos minerales que son explotados por el mismo.

Read More

Ejercicio: Leyes de Newton, plano inclinado y movimiento acelerado.

Tenemos el siguiente problema:

• El día 15 de enero de 2014 se realiza una inspección a la estación antigua y desolada de ferrocarril, encontrando en el interior una superficie plana y horizontal, que no presenta fricción. Uno de los elementos encontrados en esa superficie, es un cubo de madera, al cual se le toman los datos de posición y su masa de 0,008 kg. Se realiza una inspección posterior al lugar, el día 15 de enero de 2018 y se encuentra que el cubo de madera está a 8,00 cm de la posición marcada en la primera visita. 

Debemos calcular: 

1. La fuerza promedio del viento.
2. El ángulo que debe existir para que la caja reciba la misma fuerza aplicada por el viento.
3. Las leyes y teorías aplicas. 

Resolución:

1) Como debemos buscar la fuerza lo primero que haremos será buscar la aceleración de la caja en el periodo de los cuatro años: 

d = a·t²/2

Donde: 

• d = distancia
• a = aceleración 
• t = tiempo

Veamos que el tiempo fue de 4 años que son 1.26x10⁸ segundos, entonces:

0.08 m = a·(1.26x10⁸ s)²/2
2·(0.08m) = a·(1.26x10⁸ s)²
2·(0.08 m)/(1.26x10⁸ s)² = a

a = 1.00x10⁻¹⁷ m/s² ; siendo esta la aceleración del bloque

Aplicamos segunda ley de Newton para encontrar la fuerza promedio:

F = m·a

Donde: 

• F = fuerza
• m = masa
• a = aceleración

Entonces: 

F = (0.008 kg)·(1.00x10⁻¹⁷ m/s²)

F = 8.00x10⁻²⁰ N

Por ende, la fuerza promedio realizada por el viento fue de  8.00x10⁻²⁰ N.

2) Como debemos buscar el ángulo para que la caja sienta la misma fuerza que la del viento entonces lo que haremos será realiza una sumatoria de fuerza: 

Px = F

m·g·sen(x) = m·a

g·sen(x) = a

sen(x) = a/g

x = arcosen( 1.00x10⁻¹⁷ m/s²/ 9.8 m/s²)

x = 5.84x10⁻¹⁷ grados

Entonces, el ángulo que debería tener un plano inclinado es de 5.84x10⁻¹⁷ grados; es decir, el mismo debe aproximarse a cero.

3) Las leyes y teorías aplicadas fueron: 

• Movimiento acelerado.
• Segunda ley de Newton.
• Movimiento sobre un plano inclinado.
• Aplicación de diagrama de cuerpo libre.

Si quiere aprende más sobre estas leyes te dejo los siguientes enlaces: 

• https://300mots.blogspot.com/2020/02/leyes-de-newton-inercia-fuerza-accion-y.html
• https://300mots.blogspot.com/2020/01/ejemplo-de-movimiento-rectilineo.html

Read More

¿Qué indica el velocímetro? ¿Indica la magnitud de la velocidad media o instantánea?

El velocímetro es un instrumento que mide rapidez media, sin embargo, el intervalo de tiempo en la que se hace esta medición es tan pequeño que se aproxima la medición a la rapidez instantánea, por ende, podemos decir que el velocímetro en realidad miden el modulo de la velocidad instantánea. Los velocímetros más usados son los velocímetros digitales.

Vale mencionar que la velocidad es un vector y por ende este tiene sentido, dirección y módulo; en este caso el velocímetro solamente muestra el módulo. Veamos algunos ejemplos de velocidad:

• Un barco que viaja a 250 km/h en sentido Norte.
• Un carro que viaja a 300 km/h en sentido Sureste.
• Una avión que debe desviarse 45º Norte-Este a 150 km/h.
• Una nadador que nada a 15 km/h en sentido Norte.
• Un alpinistas que camina a 10 km/h en sentido Sureste.

Tengamos en cuenta que la rapidez es solamente un modulo, y por ende no cuenta con dirección ni sentido.

Dato curioso:

• El instrumento para medir la velocidad de automóviles que circulan se conoce como cinemómetro; por ejemplo, en las vías de Estados Unidos hay muchos de estos instrumentos que sirven para medir la velocidad de los automóviles y colocar multas por exceso de velocidad. Un cinemómetro es un instrumento muy distinto al velocímetro pero miden una misma magnitud.

Mira más información relacionada con la velocidad en:

• https://300mots.blogspot.com/2020/02/ejemplos-de-energia-cinetica-y-energia.html
• https://300mots.blogspot.com/2020/02/que-es-la-energia-cinetica-y-cual-es-su.html

Read More

Ejemplos de energía cinética y energía potencial en la vida cotidiana.

A continuación vamos a mostrar algunos ejemplos de energía cinética y energía potencial.

Ejemplos de energía cinética:

1. Una persona corriendo.
2. Un automóvil desplazándose por la autopista.
3. Un avión desplazándose en el aire.
4. Una bala al salir de la pistola.
5. Lanzar una pelota horizontalmente.

Ejemplos de energía potencial:

1. Un pelota a cierta altura del piso.
2. Una pelota en su punto más alto de trayectoria.
3. Cada vez que se sube un piso en un edificio, con cada piso adquirimos más energía potencial.
4. Cuando nos elevamos al subir una escalera.
5. Al montar un columpio y adquirir altura al balancearse.

Partiendo de los ejemplos antes mencionados podemos definir a cada energía: 

• Energía cinética: esta energía depende de la velocidad (rapidez) del objeto, y es directamente proporcional a la masa (m) y la velocidad (V).
• Energía potencial: esta energía depende de la altura respecto a una referencia, y es directamente proporcional a la masa (m) y la altura (h).

Las ecuaciones de energía potencial y energía cinética se definen como:

• Ep = m·g·h ; energía potencial
• Ec  = 0.5·m·V² ; energía cinética

Es importante mencionar que la energía no se crea ni se destruye, solamente se transforma.

Si quieres saber más sobre la energía en general te dejo los siguientes enlaces:

• https://300mots.blogspot.com/2020/02/que-es-la-energia-cinetica-y-cual-es-su.html
• https://300mots.blogspot.com/2020/02/energia-que-produce-el-agua.html

Read More

Cuál es la importancia de las ciencias sociales.

Podemos decir que la importancia de las ciencias sociales se basa en el estudio del ser humano de forma individual y de manera colectiva en una sociedad que puede llegar a ser especifica o general; de esta manera estamos definiendo qué es las ciencias sociales.

Algunos de los aspectos que podemos comprender gracias a las ciencias sociales son:

• Comportamiento del humano en la sociedad.
• Comportamiento del humano en forma individual.
• Organización social.
• Formas de comunicación de una sociedad.
• Estructuras políticas y formas de gobierno.
• Forma de comunicación entre los individuos, es decir, su lenguaje en general.
• El comportamiento del humano en una geografía y la historia del mismo.

Vale mencionar que las ciencias sociales se relaciona con muchas otras ciencias como: 

• Matemática.
• Química.
• Probabilidad.
• Estadística. 
• Biología. 
• Geografía.

Las ciencias sociales se relaciona directamente con la humanidad pues estudia al humano; la humanidad representa a todos los humanos que hacen vida en las diferentes regiones o sociedades que hay en el mundo. 

Los principales objetos de estudio de las ciencias sociales son: 

• Política.
• Etimología.
• Civismo.
• Economía.
• Historia.
• Mitología y folklore.

De esta manera conocimos algunos términos generales de lo qué es las ciencias sociales y su importancia; concluyendo que su máxima importancia se basa en estudiar a los humanos, a la humanidad.

Read More

¿Qué es la energía cinética y cuál es su fórmula?

La energía cinética es aquella forma de energía que tiene un cuerpo debido a la velocidad que adquiere. Es una de las energías que más se relaciona con la energía potencial debido a la conservación de la energía.

Tenemos que la energía cinética se calcula con la siguiente formula:

Ec = (1/2)·m·V²

Observemos como la energía cinética es una relación entre la masa (m) y la velocidad (V). Entre mayor sea la masa o velocidad de un cuerpo entonces su energía cinética será mayor.

Miremos un ejemplo de donde hay energía cinética: 

• Cuando vamos en un carro a 50 km/h, este automóvil tiene energía cinética debido a la velocidad, donde haya velocidad hay energía cinética.

Existen casos como la energía hídrica en donde se aprovecha la velocidad del agua para transformar esta energía en energía eléctrica. 

Read More

Energía que produce el agua.

La energía que produce el agua se conoce como energía HÍDRICA o HIDRÁULICA. Vale mencionar que la energía dada por el agua es energía renovable y por lo general se usa agua dulce aunque no se descartan las energías que proporciona el agua salada.

La energía que produce el agua es debido al aprovechamiento de su energía cinética y su energía potencial, aplicando la ley de conservación de la energía, lo que hace es transformarse la energía que produce el agua en otras formas de energía como la energía eléctrica.

Veamos las ecuaciones fundamentales de la energía cinética y potencial:

La energía potencial se define como: 

Ep = m·g·h

Donde: 

• Ep = energía potencial
• g = gravedad
• h = altura

La energía cinética se define como: 

Ec = (1/2)·m·V^2

Donde:

• Ec = energía cinética
• m = masa
• V = velocidad

Estas dos formas de energía son las que se transforman y obtenemos, como ya mencionamos, energía eléctrica y otras.

Esta energía la podemos observar en presas, en círculos hidráulicos conocidas como norias. En las norias se transforma la energía en trabajo, considerando que el trabajo también es energía. Vale mencionar que la energía que se obtiene del agua es energía renovable.

A continuación dejamos un ejercicio para relacionar los tipos de energía con cada imagen.

Read More

Leyes de Newton: conceptos y ejercicios.

El físico Isaac Newton planteó tres leyes fundamentales en la dinámica, estas son: ley de la inercia, ley de la fuerza y ley de acción-reacción.

Estas tres leyes son fundamentales en la física, sobre todo en el estudio de la dinámica de los cuerpos. Con estas leyes es posible entender el mundo donde vivimos y nos desarrollamos, es por ello que el conocer y entender estas leyes es fundamental para nuestra vida cotidiana y para muchas profesiones en particular.

Isaac Newton mostró estas leyes en su libro Philosophiae Naturalis Principia Mathematica o Principios Matemáticos de la Filosofía Natural. Este es uno de los libros más importantes de la historia de la humanidad.

Sir Isaac Newton. Fuente: Ejemplo.co

Leyes de Newton

Primera ley de Newton o ley de la inercia

En esta primera ley se nos plantea lo siguiente: 

• Todo cuerpo permanecerá en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado por fuerzas externas a cambiar su estado.

Es decir, Newton nos indica que todo cuerpo tiene la propiedad de evitar el cambio (el humano como tal evita el cambio, por ejemplo), por ende, se necesita de una excitación externa para que ocurra este cambio. Esta ley depende de la masa del cuerpo, entre más masa más resistencia al cambio existe. 

Ejemplos de la primera ley de Newton

1. Cuando un coche frena de manera brusca, tenemos que los pasajeros, por efecto de la inercia, se tienden a mover en la dirección en que se movía el automóvil. 
2. Cuando queremos mover una caja pesada, podemos sentir como al principio resulta difícil el mover la caja. En este caso, es la inercia la causante de evitar el movimiento de la caja.

Segunda ley de Newton o ley de la fuerza

En esta segunda ley se nos plantea lo siguiente:

• El cambio de movimiento es proporcional a la fuerza motriz externa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.

Es decir, Newton nos indica que esa excitación que debe conocer un cuerpo para que ocurra un cambio se conoce como fuerza y esta depende de la masa y la aceleración del cuerpo. Esta segunda ley nos deja la siguiente formula: 

F = m·a 

Donde: 

• F = fuerza
• m = masa
• a = aceleración

Ejemplos de la segunda ley de Newton

1. Cuando un automóvil se mueve, en este caso el motor del automóvil debe proporcionar una fuerza motriz para que se genere el movimiento del mismo. Esta fuerza le proporcionará una aceleración al automóvil.
2. Cuando se patea un balón de fútbol, en este caso el balón se mueve gracias una fuerza motriz externa que proporciona quien patea el balón.

Tercera ley de Newton o ley de acción-reacción

En esta tercera ley se nos plantea lo siguiente:

• Con toda acción ocurre siempre una reacción igual y contraria; las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentidos opuestos.

Es decir, Newton nos indica que toda acción tiene una reacción, otra forma de verlo sería: toda causa tiene su consecuencia. 

Ejemplos de la tercera ley de Newton

1. Cuando caminamos, en este caso el contacto del pie con el suelo genera una acción-reacción que nos permite caminar.
2. Cuando rebotamos una pelota contra el suelo, en este caso existe una acción-reacción entre el suelo y la pelota que permite que la misma vuelva a la mano de quien la lanzó.

Resumen de las tres leyes de Newton. Fuente: ABC.

Ejercicios relacionados con las leyes de Newton

Primer ejercicio

Si sobre una pelota de baloncesto se aplican únicamente dos fuerzas concurrentes F = 2 N y F' = 2 N de sentido contrario, ¿Cuáles son los posibles estados de dicha pelota?

Resolución:

Inicialmente lo que haremos será realizar un diagrama de cuerpo libre (DCL).

Procedemos a realizar una sumatoria de fuerza en el eje -x- para lograr encontrar la fuerza resultante.

Fr = F - F' 

Fr = 2 N - 2 N 

Fr = 0 N 

La fuerza resultante externa que se aplica sobre la pelota de baloncesto es de 0 N, por ende, el estado de la pelota es de reposo, esto considerando la primera ley de Newton.

Segundo ejercicio

Un ciclista se desplaza con una aceleración de 2 m/s² y la masa total del sistema (bicicleta más conductor) es de 65 kg, ¿Qué fuerza lleva el sistema?

Resolución: 

Para resolver este problema debemos aplicar la segunda ley de Newton, es decir, la fuerza se puede calcular como el producto entre la masa y la aceleración.

F = m·a 

F = (65 kg)·(2 m/s²) 

F = 130 N 

Por tanto, la fuerza que lleva el sistema conductor - bicicleta es de 130 N.

Tercer ejercicio

Un automóvil choca contra otro con un vector fuerza de (1,-5) N, ¿Cuál es el vector reacción? 

Resolución: 

Inicialmente planteamos el diagrama de cuerpo libre (DCL).

Aplicando la teoría de la tercera ley de Newton, sabemos que la reacción de una fuerza tiene la misma dirección pero el sentido es contrario.

F = - F' 

F = -(1, -5) N

F = (-1,5) N

Por tanto, la fuerza de reacción que hubo en el choque es igual a (-1,5) N.

Referencias: 

1. Enciclopedia de Ejemplos (2019). "Leyes de Newton"
2. Tipler, P. 2010. Física. Volumen 1. 5ta Edición. Editorial Reverté. 94 – 95.

Read More

Tres datos curiosos de cultura general.

A continuación verás tres datos curiosos de cultura general que te ayudarán a ser más culto:

• ¿Sabias que las nutrias tienen una piedra favorita? Si, tienen una piedra favorita, además estos cuando no la usan la guardan en un bolsillo que tienen en el brazo para no extraviar a la misma.  

• Un bebe tiene, de manera aproximada, 100 huesos más que una persona adulta. Es por ello que cuando somos pequeños tenemos mayor flexibilidad que cuando somos adultos. 

• Si tus ojos fueran una cámara entonces sería de 576 megapíxeles, increíble. ¿De cuántos píxeles es la cámara de tu teléfono?

Read More

Qué civilización nos dejó la democracia, ¿Qué es la democracia?

Podemos decir que la civilización griega fue la que nos lego la democracia. La democracia tiene su origen en Atenas.

La civilización griega fue una de las más grandes y desarrolladas en su época, se enfocaron mucho en la ciencia y la filosofía, pues le interesaba el comportamiento natural.

Ademas, desarrollaron el arte generando grandes pinturas y arquitectura. Por otra parte, los griegos eran politeístas, es decir, creían en muchos seres divinos.

Pero, ¿qué es la democracia? Es complicado definir la democracia, sin embargo todo se ajusta a una forma de gobierno donde el pueblo participa de manera directa. Hoy en día ninguna democracia existente plantea la democracia que se desarrollaba en Grecia.

Aunque los Estados actuales se inclinan por una democracia participativa tenemos que estas no son realmente participativas porque el pueblo y la sociedad no esta totalmente involucrada en la política.

Read More

¿Cuántos huesos tiene una gallina?

Podemos decir que una gallina adulta tiene consigo 31 huesos, sin embargo, dependiendo la especie, pudiera variar este número.

Dependiendo el animal y la especie tenemos que la cantidad de huesos suele cambiar.

Por ejemplo, un humano puede tener entre 206-208 huesos, cuando todos estos huesos se juntan debido a diferentes articulaciones se genera lo que es el esqueleto. Los huesos son fundamentales para la movilidad.

Veamos algunas ventajas de tener huesos y esqueleto: 

1. La estructura del cuerpo es más sólida.
2. Se puede tener mayor movilidad en el organismo.
3. Los huesos protegen a muchos órganos blandos, por ejemplo, las costillas protegen a los pulmones. 

En la imagen podemos ver los principales huesos que tiene una gallina adulta común.

Read More

Alimentos que contienen aluminio.

Podemos decir que el pepino, el pepinillo, la zanahoria, carne, huevo y algunos té son alimentos que contienen aluminio. Tengamos en cuenta que estos alimentos tienen consigo aluminio natural.

Es importante mencionar que el aluminio es el metal de color blanco brillante, el cual es utilizado en el envase de alimentos para su conservación.

El aluminio es un metal resistente a la oxidación, esta es una razón por la cual se usa este elemento para almacenar alimentos, ya que no se contamina.


Algunas propiedades del aluminio son:

• Símbolo: Al
• Densidad: 2.7 g/cc
• Punto de fusión: 660ºC 
• Punto de ebullición: 2450ºC 

El cuerpo humano requiere de muchos metales que son importantes para nuestra salud integral, sin embargo debemos consumir estos metales partiendo de diferentes alimentos.

Read More

Ejemplo de movimiento rectilíneo uniformemente acelerado

En este caso veremos un ejemplo de un movimiento rectilíneo uniformemente acelerado (MRUVA y veremos las características de la velocidad y la aceleración para este ejemplo. 

• Ejemplo:  Un automóvil que se desplaza en la autopista, en linea recta, aumentando su velocidad.

La velocidad y la aceleración, de este ejemplo, tienen las siguientes características:

1. La velocidad aumenta y la aceleración se mantiene constate.
2. Para el caso del ejemplo tenemos que el vector velocidad y aceleración tienen el mismo sentido y dirección (esto no siempre es así).

NOTA: existen casos en donde la aceleración tiene un sentido contrario a la velocidad cuando esto ocurre existe un movimiento acelerado pero se esta frenando, esto es fundamental conocerlo para asignarle el signo adecuado a la aceleración. 

Read More